05 - Les SIF

Question 1

Pour chacune des paires d’ensembles ci-dessous, trouvez \(d_H(A,B)\), où \(d_H\) est la distance de Hausdorff.

1. \(A = \{(x_1,y_1)\}\) et \(B = \{(x_2,y_2)\}\).

   Solution. \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)

2. \(A = \{(1,1)\}\) et \(B = \{(x,y) : x^2 + y^2 \leq r^2\}\).

   Solution. \(r + \sqrt{2}\)

3. \(A = \{(x,0) : -1 \leq x \leq 1\}\) et \(B = \{(0,y) : -2 \leq y \leq 2\}\).

   Solution. \(2\)

4. \(A = \{(x,y) : (x - h_1)^2 + (y - k_1)^2 \leq r_1^2\}\) et \(B = \{(x,y) : (x - h_2)^2 + (y - k_2)^2 \leq r_2^2\}\).

   Solution. \(\sqrt{(h_2 - h_1)^2 + (k_2 - k_1)^2} + |r_2 - r_1|\)

Question 2

Un SIF est formé de deux similitudes de rapport \(\frac{1}{2}\), et de trois similitudes de rapport \(\frac{1}{4}\).

1. Quel est le rapport de contraction du SIF ?

   Solution. \(\frac{1}{2}\)

2. Quelle est la dimension de similitude généralisée de l’attracteur du SIF ?

   Solution. \(\frac{\ln 3}{\ln 2}\)

3. Si le SIF avait plutôt été formé de deux contractions de rapport \(\frac{1}{2}\), et de trois contractions de rapport \(\frac{1}{3}\), quelle aurait été la dimension de similitude généralisée de son attracteur ?

   Solution. On ne peut trouver la valeur exacte. Une valeur approchée serait \(d \approx 1{,}788\).

Question 3

Pour chacun des ensembles \(E\) autosimilaires ci-dessous :

1. Trouvez les transformations \(w_i\) telles que \(E\) est l’attracteur du SIF \(\{w_i\}_{i \in J}\), où \(J = \{1,2,\ldots,n\}\) pour un certain \(n \in \mathbb{N}\);
2. Utilisez un ordinateur pour construire une image qui ressemble à \(E\);
3. Trouvez, si elle existe, la dimension de similitude de \(E\);
4. Trouvez, si elle existe, la dimension de similitude généralisée de \(E\).

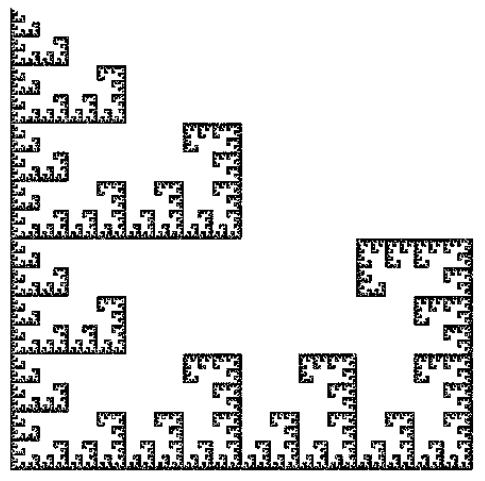
Question 4

Soit \(\mathcal{S}\) le SIF dont l’attracteur est représenté ci-dessous.

Fractale

1. Trouvez 3 fonctions \(f_1, f_2\) et \(f_3\) telles que \(\mathcal{S} = \{f_1,f_2,f_3\}\).

   Solution. On trouve que \[ f_1\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} \frac{1}{2} & 0 \\ 0 & \frac{1}{2} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}, \quad f_2\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} \frac{1}{2} & 0 \\ 0 & \frac{1}{2} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 8 \\ 0 \end{pmatrix}. \] Pour \(f_3\), c’est la composée d’une rotation \(r\), d’une contraction \(c\) et d’une translation \(t\). Ainsi, \[ f_3\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 & -\frac{4}{5} \\ \frac{5}{16} & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 16 \\ 5 \end{pmatrix}. \]

2. Quelle est la dimension de similitude généralisée de \(A\)?

   Solution. Dans cette situation, nous ne sommes pas en mesure de déterminer la dimension de similitude de cet ensemble, ni même la dimension de similitude généralisée. En effet, l’une des transformations n’est pas une similitude.

Question 5

Considérons le SIF formé des contractions \[ w_1\begin{pmatrix} x \\ y \end{pmatrix} = \frac{1}{3} \begin{pmatrix} x \\ y \end{pmatrix}, \quad w_2\begin{pmatrix} x \\ y \end{pmatrix} = \frac{1}{3} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} \frac{2}{3} \\ 0 \end{pmatrix}. \]

Soit \(C = \{(x,y) : x,y \in [0,1]\}\).

1. Représentez \(C\) dans le plan.

   Solution.

   

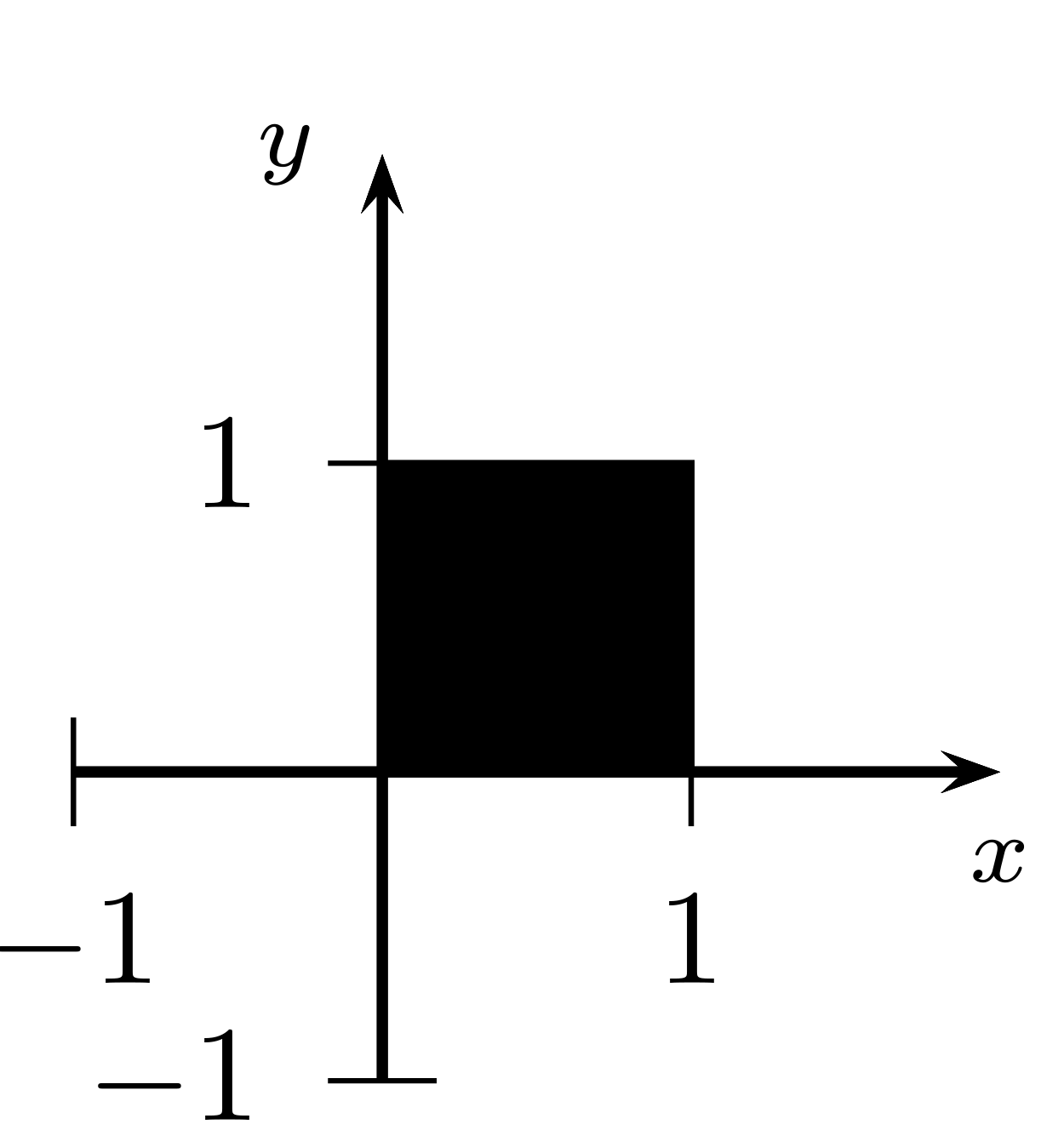
   Ensemble C

2. Trouvez \(W(C)\) et le représenter dans le plan.

   Solution.

   

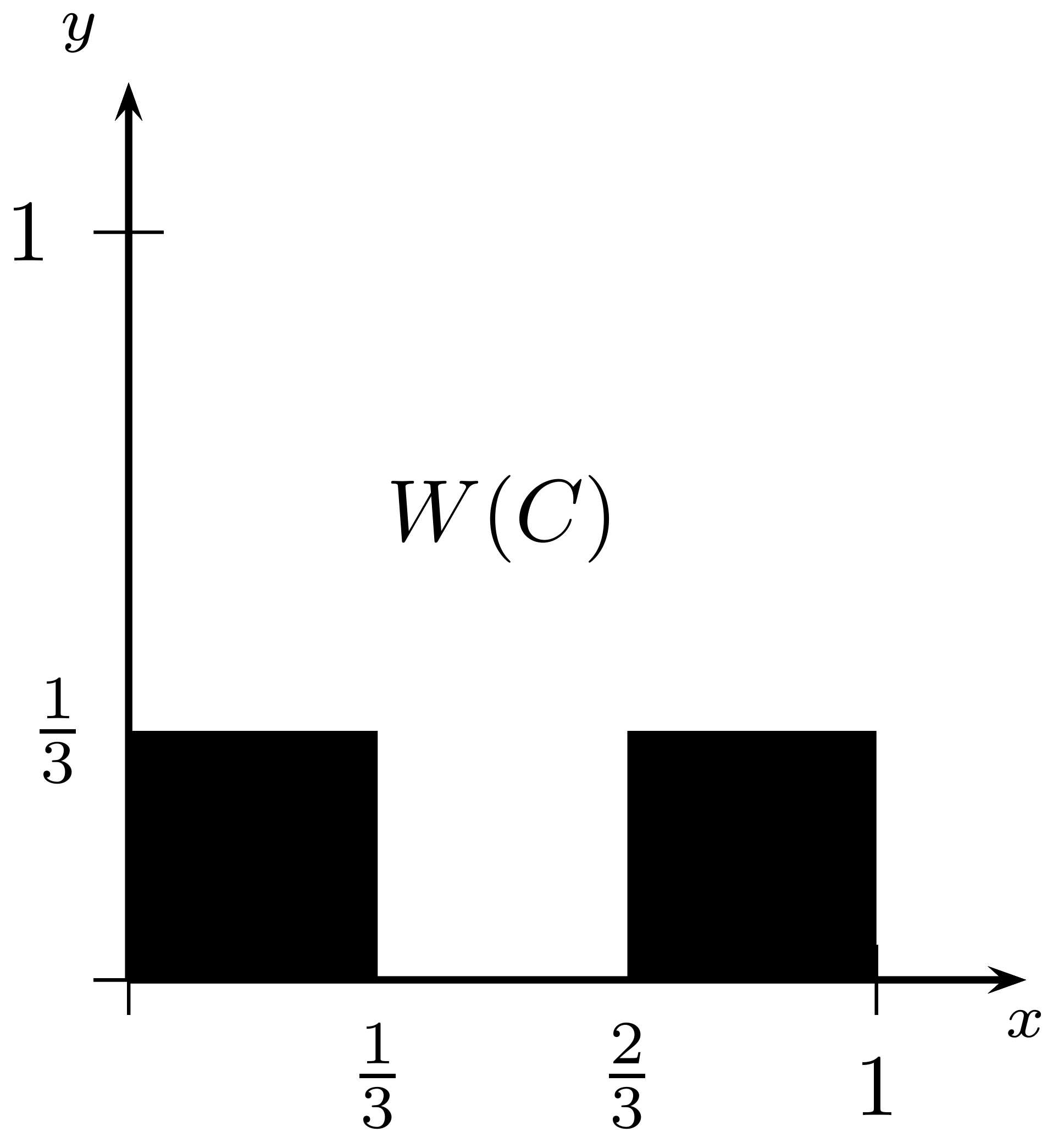
   Ensemble W(C)

3. Trouvez \(W^{2}(C)\) et le représenter dans le plan.

   Solution.

   

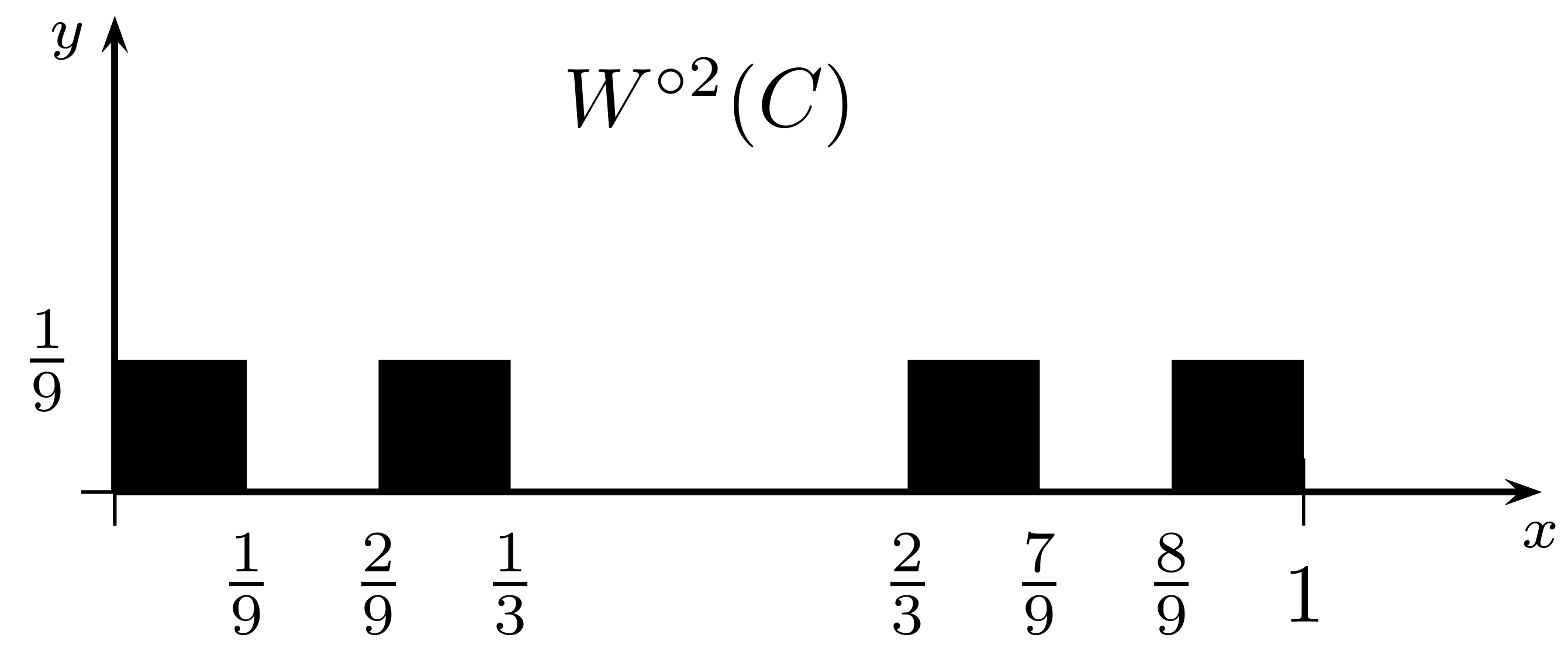
   Ensemble \(W^{2}(C)\)

4. Que vaut \(d_H(W(C),C)\)?

   Solution. Du dessin ci-dessous, on déduit que \(d_H(W(C),C) = \frac{\sqrt{17}}{6}\).

   

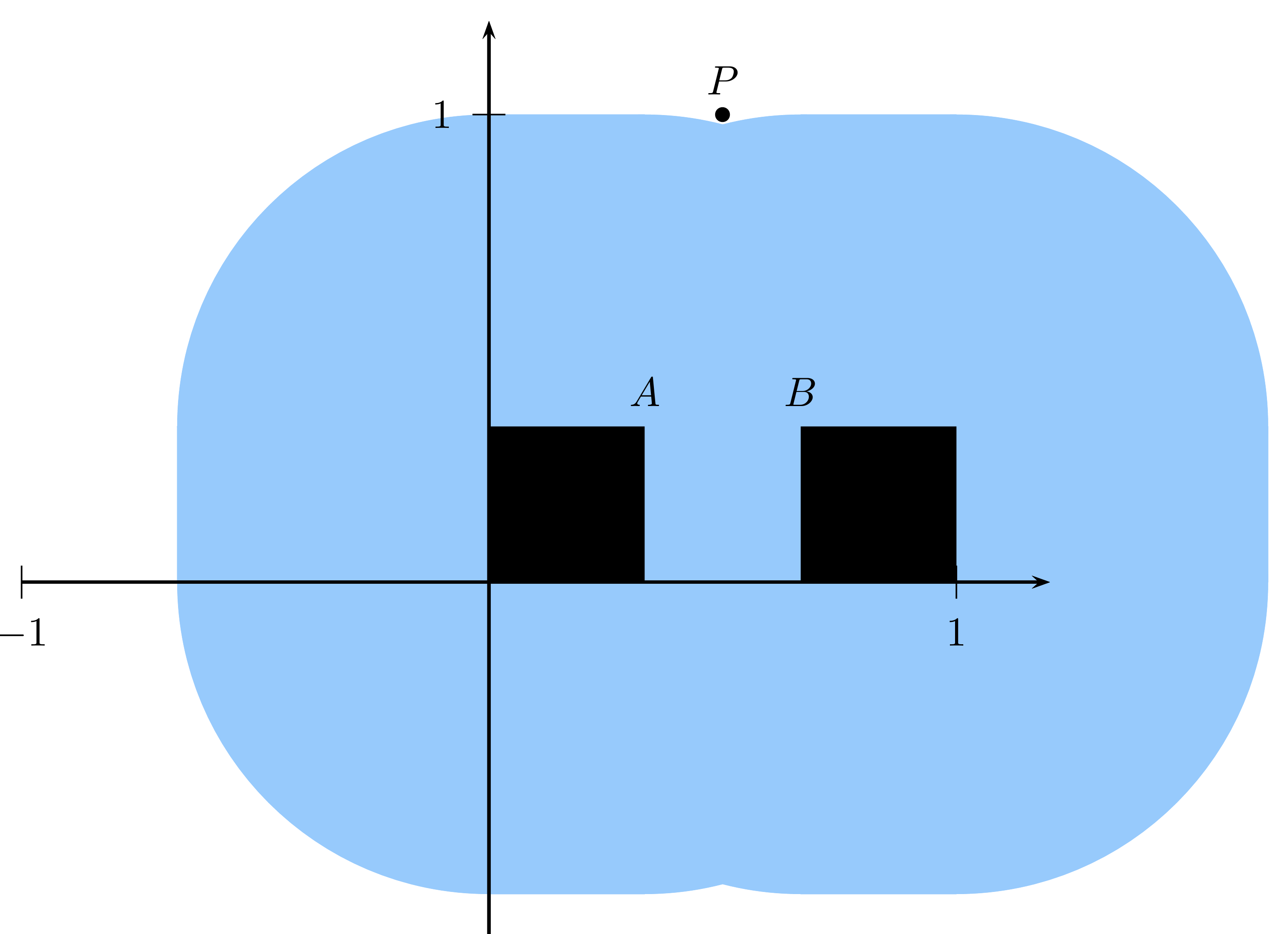
   Le point P est le point de C le plus éloigné des points appartenant à W(C).

5. Que vaut le rapport de contraction du SIF ?

   Solution. \(\frac{1}{3}\)

6. Soit \(A\) l’attracteur du SIF considéré. Utilisez le théorème de Hutchinson pour trouver une valeur de \(n\) telle que \[ d_{H}\left(W^{n}(C),A\right) \leq 0{,}01. \]

   Solution. On doit choisir \(n \geq 5\).

Question 6 (Défi facultatif)

Répondez aux sous-questions de la question 3 pour la figure ci-dessous.

Fougère de Barnsley