11 - Processus stochastiques (2/3)
Question 1
Construisez une procédure qui prend comme entrée un vecteur \(\vec{v}\), et qui retourne un vecteur de probabilités colinéaire à \(\vec{v}\).
Question 2
Dans une ville, on a remarqué qu’il y avait trois types de véhicules :
- les automobiles de type berlines et coupés (A) ;
- les véhicules utilitaires sportifs (V);
- les camionnettes (C).
Chaque année, on observe les transitions suivantes :
- \(3\%\) des propriétaires de (A) échangent leur (A) pour un (V), et \(1\%\) échangent leur (A) pour un (C) ;
- \(2\%\) des propriétaires d’un (V) échangent leur (V) pour un (A), et \(3\%\) échangent leur (V) pour un (C) ;
- \(5\%\) des propriétaires d’un (C) échangent leur (C) pour un (V), et \(2\%\) échangent leur (C) pour un (A).
Actuellement, les proportions sont de :
- \(65\%\) pour (A),
- \(30\%\) pour (V),
- \(5\%\) pour (C).
En supposant que le nombre de véhicules reste constant, déterminez les proportions de (A), (V), et (C) dans :
- 1 an ;
- 5 ans ;
- 10 ans ;
- À long terme.
Question 3
(Source: Wikipédia)
Doudou, le hamster paresseux, connaît trois endroits dans sa cage : les copeaux où il dort, la mangeoire où il mange, et la roue où il fait de l’exercice. Ses journées sont assez semblables les unes aux autres, et son activité peut être modélisée par une chaîne de Markov.
Les probabilités de transition sont les suivantes :
- Quand il dort, il a \(9/10\) de chances de ne pas se réveiller. Lorsqu’il se réveille, il a \(1/2\) de chances d’aller manger et \(1/2\) de chances de faire de l’exercice.
- Après avoir mangé, il a \(7/10\) de chances de retourner dormir et \(3/10\) de chances de partir courir.
- Après avoir couru, il a \(8/10\) de chances de retourner dormir, sinon il continue à courir.
Combien de temps Doudou passe-t-il à dormir en moyenne dans une journée ?
Question 4
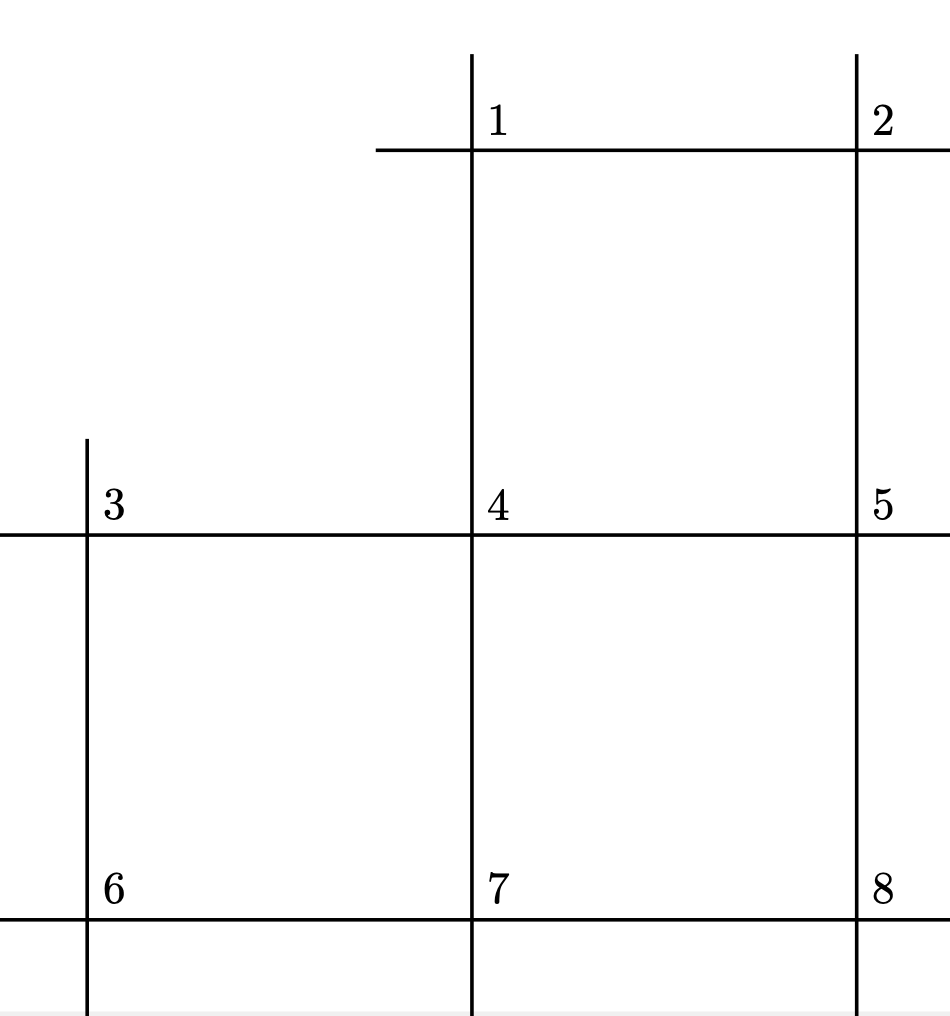
Un policier contrôle la circulation aux 8 intersections illustrées ci-dessous. Lorsqu’il arrive à une intersection, il y demeure une heure, puis décide aléatoirement d’aller à une intersection voisine ou de rester à celle où il est. Chaque possibilité a la même probabilité d’être choisie. Par exemple :
- S’il est à l’intersection 5, il peut choisir d’aller à 2, 4, 5 ou 8, avec une probabilité de \(1/4\) pour chacune.
À la fin de sa journée de travail, il choisit une intersection voisine (ou la même) comme point de départ pour le lendemain. Déterminez le pourcentage de son temps de travail qu’il passe à chacune des intersections.