01 - Introduction aux fractales

Question 1

On construit un flocon de von Koch à partir d’un triangle équilatéral dont les côtés sont de longueur 1.

Flocon de von Koch

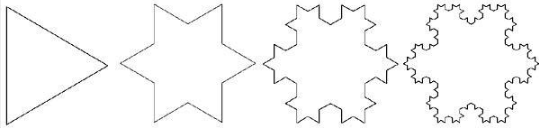
1. Montrez que le périmètre du flocon est infini.

2. Déterminez l’aire du flocon.

Solution.

1. Le périmètre du flocon est multiplié par \(\frac{4}{3}\) à chaque étape de la construction. Par conséquent, le périmètre est infini.

2. L’aire du flocon est donnée par : \[ \text{Aire finale} = \frac{8}{5} A_0, \] où \(A_0\) est l’aire du triangle équilatéral initial. Par exemple, pour un triangle dont les côtés mesurent 1, l’aire du flocon est \(\frac{2\sqrt{3}}{5}\).

Question 2

On construit un flocon de neige à partir d’un carré de côté de longueur \(a\).

Flocon de neige

1. Trouvez l’aire du flocon après \(n\) étapes.

2. Déterminez la dimension de similitude du flocon de neige.

Solution.

1. Si \(A_1 = a^2\) est l’aire après une étape, nous avons : \[ A_n = \left(\frac{5}{9}\right)^{n-1} a^2. \]

2. La dimension de similitude est donnée par : \[ \frac{\ln 5}{\ln 3}. \]

Question 3

Soit \(E\) l’ensemble des nombres réels dans l’intervalle \([0, 1]\) dont toutes les décimales sont paires.

1. Expliquez comment on peut contruire l’ensemble \(E\) et débutant avec l’intervalle \([0, 1]\) duquel on retranche, à chaque étape, des intervalles.

2. Expliquez pourquoi \(E\) est autosimilaire puis calculez sa dimension de similitude.

Solution.

1. On construit \(E\) en retirant, à l’étape \(n\), les nombres dont la \(n^\text{e}\) décimale est impaire.

2. Sa dimension de similitude est : \[ \frac{\ln 5}{\ln 10}. \]

Question 4

Pour chacun des ensembles autosimilaires suivants, déterminez son aire, de même que sa dimension de similitude.

1. Le triangle de Sierpiński construit à partir d’un triangle équilatéral dont les côtés sont de longueur 1.

2. Le tapis de Sierpiński construit à partir d’un carré dont les côtés sont de longueur 1.

Solution.

1. L’aire est nulle et la dimension de similitude est \(\frac{\ln 3}{\ln 2}\).

2. L’aire est nulle et la dimension de similitude est \(\frac{\ln 8}{\ln 3}\).

Question 5

Pour chacun des ensembles autosimilaires suivants, déterminez son volume, de même que sa dimension de similitude.

1. L’éponge de Menger construite à partir d’un cube dont les arêtes sont de longueur 1.

2. Le tétraèdre de Sierpiński construit à partir d’un tétraèdre dont les arêtes sont de longueur 1.

Solution.

1. Le volume est nul et la dimension de similitude est \(\frac{\ln 20}{\ln 3}\).

2. Le volume est nul et la dimension de similitude est \(2\).