12 - Processus stochastiques (3/3)
Indication
Pour certaines questions, vous êtes encouragés à utiliser un outil informatique pour faire les calculs.
Question 1
La matrice suivante est la matrice de transition d’une chaîne de Markov associée à un mini-web :
\[ \begin{pmatrix} 0 & \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{1}{3} & 0 & 0 & 0 \\ \frac{1}{3} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{3} & 0 & \frac{1}{2} & 0 \end{pmatrix} \]
Donnez une représentation schématique du mini-web.
Solution. 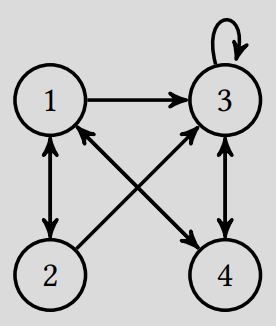
Question 2
Considérez le mini-web suivant :
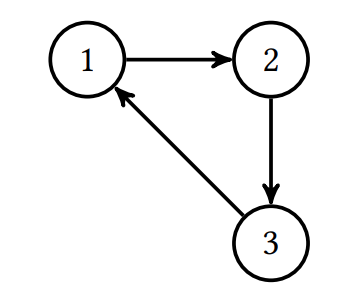
- Sans faire de calculs, déterminez le PageRank du mini-web.
- Pouvez-vous ajouter d’autres liens tout en conservant le même PageRank ?
Solution.
Puisqu’un promeneur se déplace en suivant les liens et passe autant de temps sur chaque page, le PageRank est \[ 1 \cong 2 \cong 3. \]
On peut ajouter des liens de manière symétrique pour conserver le même PageRank. Par exemple :
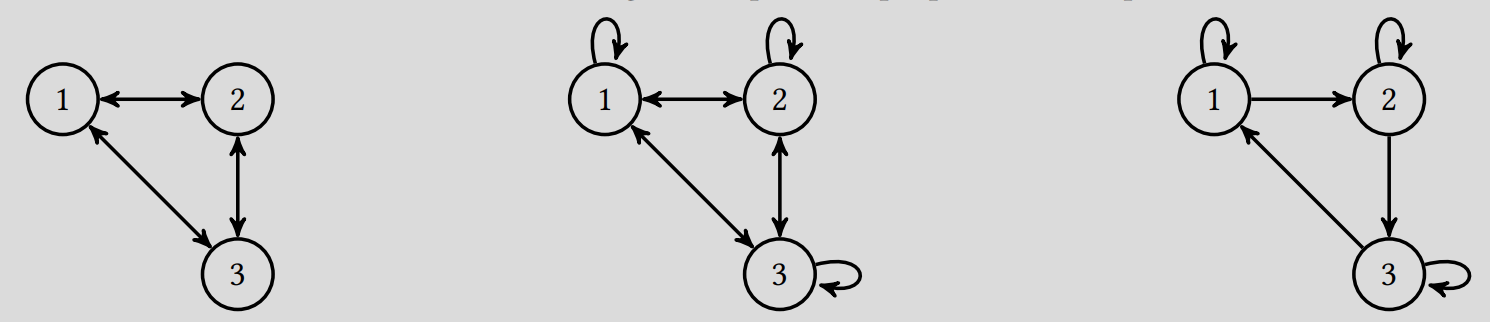
Question 3
Soit \(\mathcal{W}\) le mini-web suivant :
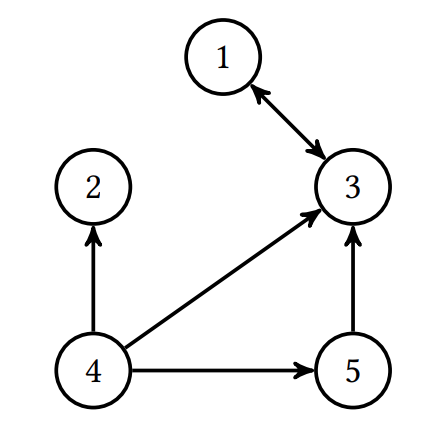
- Si un promeneur débute à la page 5, quel sera son PageRank ?
- Que se passe-t-il s’il débute à la page 2 ?
- Déterminez la matrice de transition de \(\mathcal{W}\).
- Trouvez un vecteur \(\vec{v}\) tel que \(M\vec{v} = \vec{v}\).
- Trouvez le polynôme caractéristique de \(M\).
- Trouvez les valeurs propres de \(M\).
- Modifiez la matrice pour tenir compte des pages sans liens sortants. Appelez cette matrice \(N\).
- Calculez la matrice Google \(G\) avec une probabilité de téléportation \(\frac{1}{10}\).
- Utilisez \(G\) pour déterminer le PageRank.
Question 4
Considérez le mini-web \(\mathcal{W}\) ci-dessous.
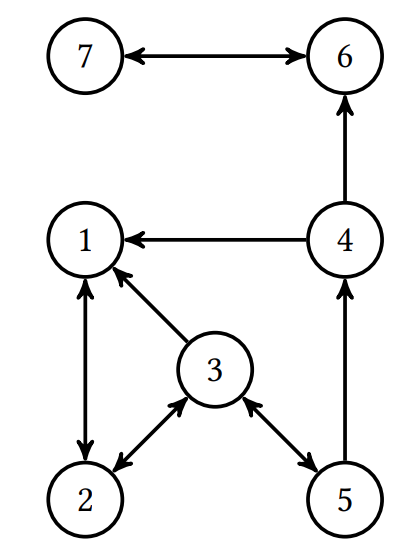
- Trouvez la matrice de transition de \(\mathcal{W}\).
- Trouvez la matrice de transition de \(\mathcal{W}\) qui permet la téléportation avec probabilité 0.15.
- À l’aide d’un outil informatique, trouvez le PageRank de \(\mathcal{W}\) (en utilisant la matrice trouvée en 2).
Question 5
Considérez un mini-web \(\mathcal{W}\) avec \(N\) pages, où \(N \geq 2\). Les vecteurs \(\vec{e}\) et \(\vec{E}\) sont définis par :
\[ \vec{e} = \begin{pmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{pmatrix}, \quad \vec{E} = \begin{pmatrix} E_1 \\ E_2 \\ \vdots \\ E_N \end{pmatrix}, \quad E_i = \begin{cases} 1 & \text{si la page } i \text{ n'a pas de liens sortants}, \\ 0 & \text{sinon.} \end{cases} \]
- À quoi correspond \(\frac{1}{N}\vec{e}\vec{E}^T\)?
- Si \(A\) est la matrice de transition, exprimez \(B\) pour tenir compte des pages sans liens sortants.
- Montrez que la matrice Google \(G\), avec une probabilité \(\beta\), peut s’exprimer : \[ G = \beta A + \frac{1}{N} \vec{e} (\beta \vec{E}^T + (1 - \beta)\vec{e}^T). \]
- Pourquoi \(A\) est une matrice creuse ? Pourquoi \(G\) est une matrice où tous les éléments sont dans \(]0, 1[\) ?