---
title: "03 - Espaces métriques"
author: "Jérôme Soucy"
---
## Question 1
Soit $P(x_1,y_1)$ et $Q(x_2,y_2)$ des éléments de $\mathbb{R}^2$. Déterminez si les fonctions suivantes sont des métriques sur $\mathbb{R}^2$. Dans chacun des cas, justifiez votre réponse.
1. $d(P,Q) = |x_1-x_2| + |y_1-y_2|$
::: solution
Oui, c'est la distance euclidienne.
:::
2. $d(P,Q) = |x_1-x_2| \cdot |y_1-y_2|$
::: solution
Non, par exemple $d((1,0),(1,1))=0$ alors que les points $(1,0)$ et $(1,1)$ sont distincts. Cela contredit la propriété d'une métrique voulant que $d(P,Q)=0\Rightarrow P=Q$.
:::
3. $d(P,Q) = |x_1+x_2| + |y_1+y_2|$
::: solution
Non, par exemple $d((1,0),(-1,0))=0$ alors que les points $(1,0)$ et $(-1,0)$ sont distincts. Cela contredit la propriété d'une métrique voulant que $d(P,Q)=0\Rightarrow P=Q$.
:::
## Question 2
Soit l'espace métrique $\left(\mathbb{R}^2,d\right)$, où $d$ est la métrique définie par
$$
d\left((x_1,y_1),(x_2,y_2)\right) = |x_1-x_2| + 2|y_1-y_2|.
$$
Dessinez la boule ouverte centrée à l'origine de rayon $r$.
::: solution
L'intérieur du losange de sommets $\left(0,\frac{1}{2}\right), \left(1,0\right), \left(0,-\frac{1}{2}\right), \left(-1,0\right)$.
:::
## Question 3
Est-ce que l'espace métrique $\left(\mathbb{R} \setminus \mathbb{Q}, d_E\right)$ est complet? Justifiez.
::: solution
Non. Il suffit de considérer une suite de nombres irrationnels qui converge vers un nombre rationnels. Par exemple, la suite $(x_n)$ où $x_n=\frac{\sqrt{2}}{n}$ est une suite de Cauchy dans $\mathbb{R} \setminus \mathbb{Q}$ qui converge vers $0$, un nombre qui n'est pas dans cet ensemble.
:::
## Question 4
Donnez le terme général d'une suite $(x_n)$ de nombres rationnels qui converge vers $\sqrt{2}$, faisant de $\left(\mathbb{Q}, d_E\right)$ un espace métrique qui n'est pas complet.
::: solution
Plusieurs réponses possibles, le graphe de la fonction $f(x)=x^2-2$ et la construction de tangentes bien choisies peut vous suggérer une méthode.
:::
## Question 5
Vrai ou faux avec justification. Soit $(x_n)$ une suite dans un espace métrique $\left(E,d\right)$. Si
$$
d(x_n,a) < \frac{1}{n} \text{ pour tout } n \geq 1000,
$$
alors $a \in E$.
::: solution
Faux, la suite considérée à la question 3 fourni un contre-exemple.
:::
## Question 6
Pour chacun des ensembles ci-dessous, considérés dans l'espace métrique $\left(\mathbb{R}^2, d_E\right)$, déterminez lesquelles des caractéristiques suivantes sont possédées par l'ensemble : **Fermé**, **Ouvert**, **Borné**, **Compact**. Donnez aussi une représentation graphique de l'ensemble.
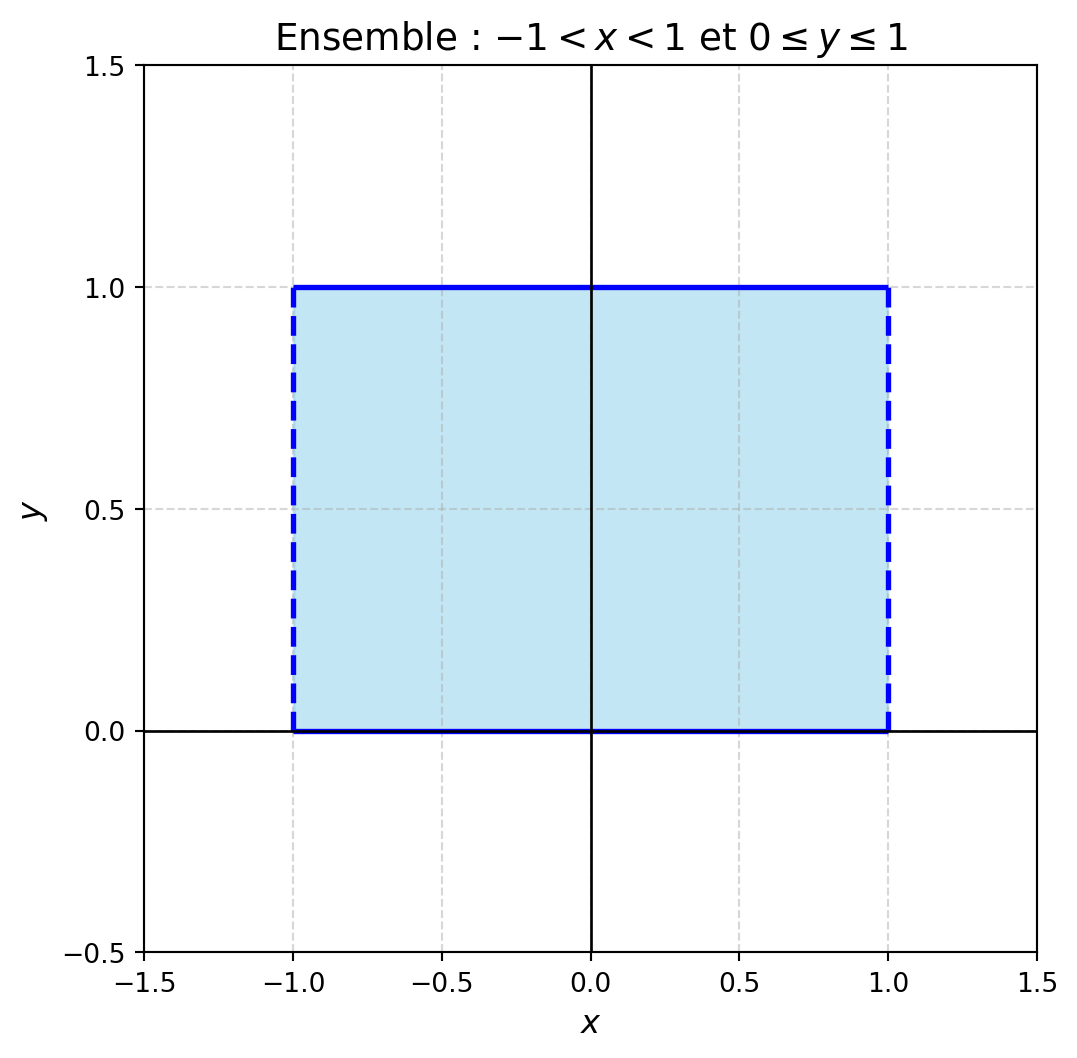
1. $\left\{(x,y)\in\mathbb{R}^2 : -1 < x < 1 ~\text{et}~ 0 \leq y \leq 1\right\}$
::: solution
Borné
```{python}
import matplotlib.pyplot as plt
import numpy as np
# Création de la figure et des axes
fig, ax = plt.subplots(figsize=(6, 6))
# Dessiner la région remplie entre x = -1 et x = 1, y entre 0 et 1
x_fill = np.linspace(-1, 1, 1000) # Points pour remplir le rectangle
y_bottom = np.zeros_like(x_fill) # Bas de la région y = 0
y_top = np.ones_like(x_fill) # Haut de la région y = 1
ax.fill_between(x_fill, y_bottom, y_top, where=(x_fill > -1) & (x_fill < 1),
color='skyblue', alpha=0.5, label='-1 < x < 1, 0 ≤ y ≤ 1')
# Tracer les segments horizontaux (inclus dans l'ensemble)
ax.hlines(y=0, xmin=-1, xmax=1, color='blue', linestyle='-', linewidth=2)
ax.hlines(y=1, xmin=-1, xmax=1, color='blue', linestyle='-', linewidth=2)
# Tracer les lignes verticales pointillées aux limites x = -1 et x = 1 dans y ∈ [0, 1]
y_vertical = np.linspace(0, 1, 100) # y de 0 à 1
ax.plot([-1] * len(y_vertical), y_vertical, 'b--', linewidth=2) # x = -1
ax.plot([1] * len(y_vertical), y_vertical, 'b--', linewidth=2) # x = 1
# Ajouter les axes x et y qui s'intersectent en (0,0)
ax.axhline(0, color='black', linewidth=1) # Axe des x
ax.axvline(0, color='black', linewidth=1) # Axe des y
# Configuration des limites et des graduations
ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-0.5, 1.5)
ax.set_xticks(np.arange(-1.5, 1.6, 0.5)) # Graduations sur x
ax.set_yticks(np.arange(-0.5, 1.6, 0.5)) # Graduations sur y
# Étiquettes des axes
ax.set_xlabel('$x$', fontsize=12)
ax.set_ylabel('$y$', fontsize=12)
ax.set_title(r"Ensemble : $-1 < x < 1$ et $0 \leq y \leq 1$", fontsize=14)
# Affichage de la grille pour une meilleure lisibilité
ax.grid(True, linestyle='--', alpha=0.5)
# Affichage du graphique
plt.show()
```
:::
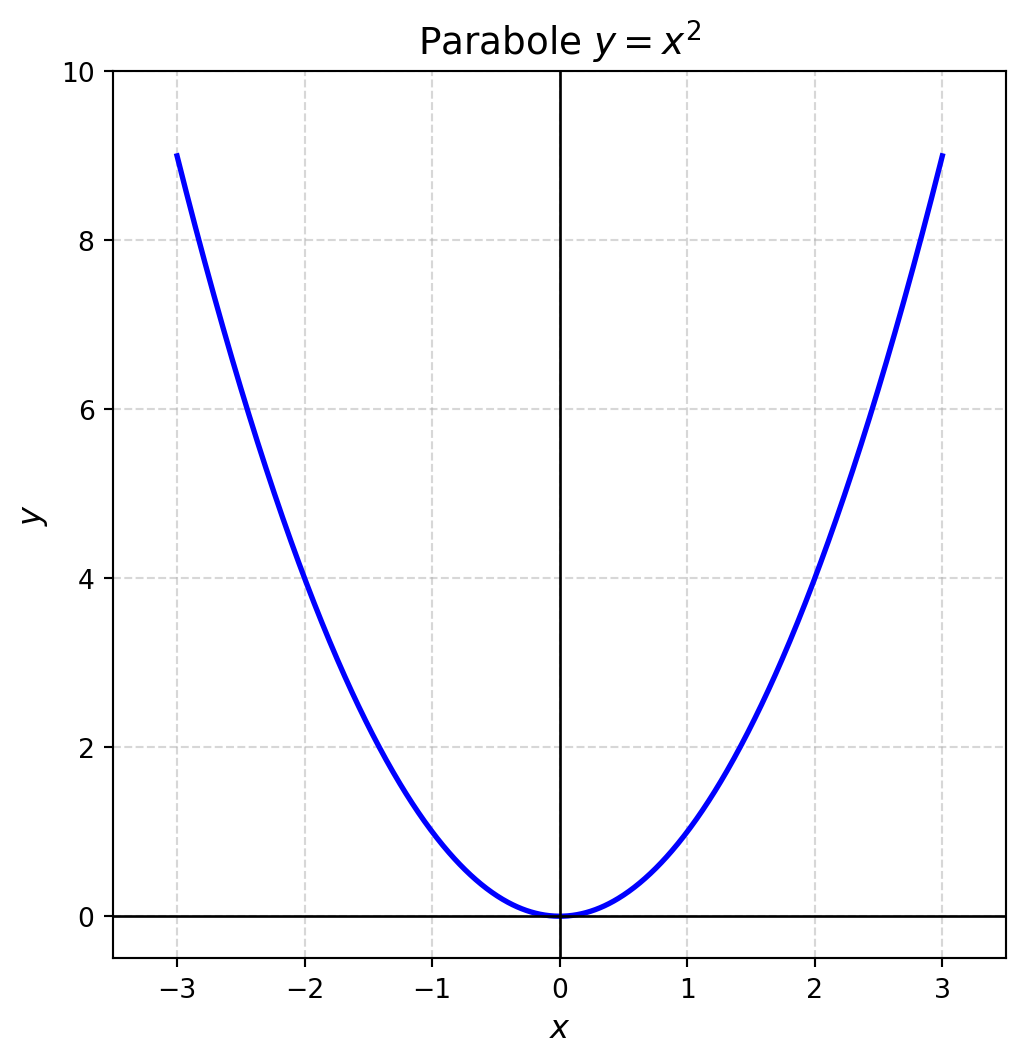
2. $\left\{(x,y)\in\mathbb{R}^2 : y = x^2\right\}$
::: solution
Fermé
```{python}
import matplotlib.pyplot as plt
import numpy as np
# Création de la figure et des axes
fig, ax = plt.subplots(figsize=(6, 6))
# Définir les données pour la parabole y = x^2
x = np.linspace(-3, 3, 1000) # Points entre -3 et 3
y = x**2 # Parabole
# Tracer la parabole
ax.plot(x, y, color='blue', linewidth=2)
# Ajouter les axes x et y qui s'intersectent en (0, 0)
ax.axhline(0, color='black', linewidth=1) # Axe des x
ax.axvline(0, color='black', linewidth=1) # Axe des y
# Configuration des limites et des graduations
ax.set_xlim(-3.5, 3.5)
ax.set_ylim(-0.5, 10)
ax.set_xticks(np.arange(-3, 4, 1)) # Graduations sur x
ax.set_yticks(np.arange(0, 11, 2)) # Graduations sur y
# Étiquettes des axes
ax.set_xlabel('$x$', fontsize=12)
ax.set_ylabel('$y$', fontsize=12)
ax.set_title(r"Parabole $y = x^2$", fontsize=14)
# Affichage de la grille pour une meilleure lisibilité
ax.grid(True, linestyle='--', alpha=0.5)
# Affichage du graphique
plt.show()
```
:::
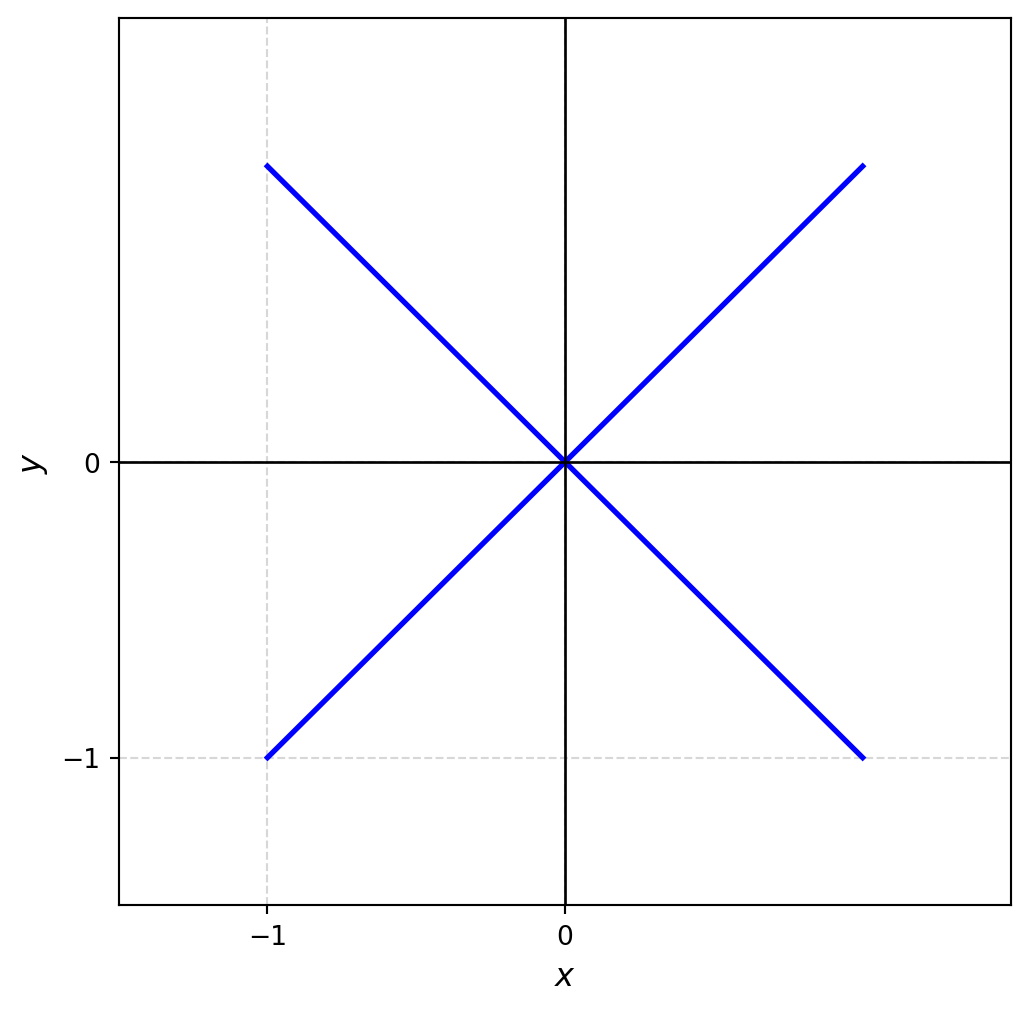
3. $\left\{(x,y)\in\mathbb{R}^2 : |x| = |y| ~\text{et}~ -1 \leq x \leq 1\right\}$
::: solution
Borné, fermé et compact
```{python}
import matplotlib.pyplot as plt
import numpy as np
# Création de la figure et des axes
fig, ax = plt.subplots(figsize=(6, 6))
x = np.linspace(-1, 1, 1000) # Points entre -3 et 3
y = x
# Tracer la parabole
ax.plot(x, y, color='blue', linewidth=2)
y=-x
ax.plot(x, y, color='blue', linewidth=2)
# Ajouter les axes x et y qui s'intersectent en (0, 0)
ax.axhline(0, color='black', linewidth=1) # Axe des x
ax.axvline(0, color='black', linewidth=1) # Axe des y
# Configuration des limites et des graduations
ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-1.5, 1.5)
ax.set_xticks(np.arange(-1, 1, 1)) # Graduations sur x
ax.set_yticks(np.arange(-1, 1, 1)) # Graduations sur y
# Étiquettes des axes
ax.set_xlabel('$x$', fontsize=12)
ax.set_ylabel('$y$', fontsize=12)
# Affichage de la grille pour une meilleure lisibilité
ax.grid(True, linestyle='--', alpha=0.5)
# Affichage du graphique
plt.show()
```
:::
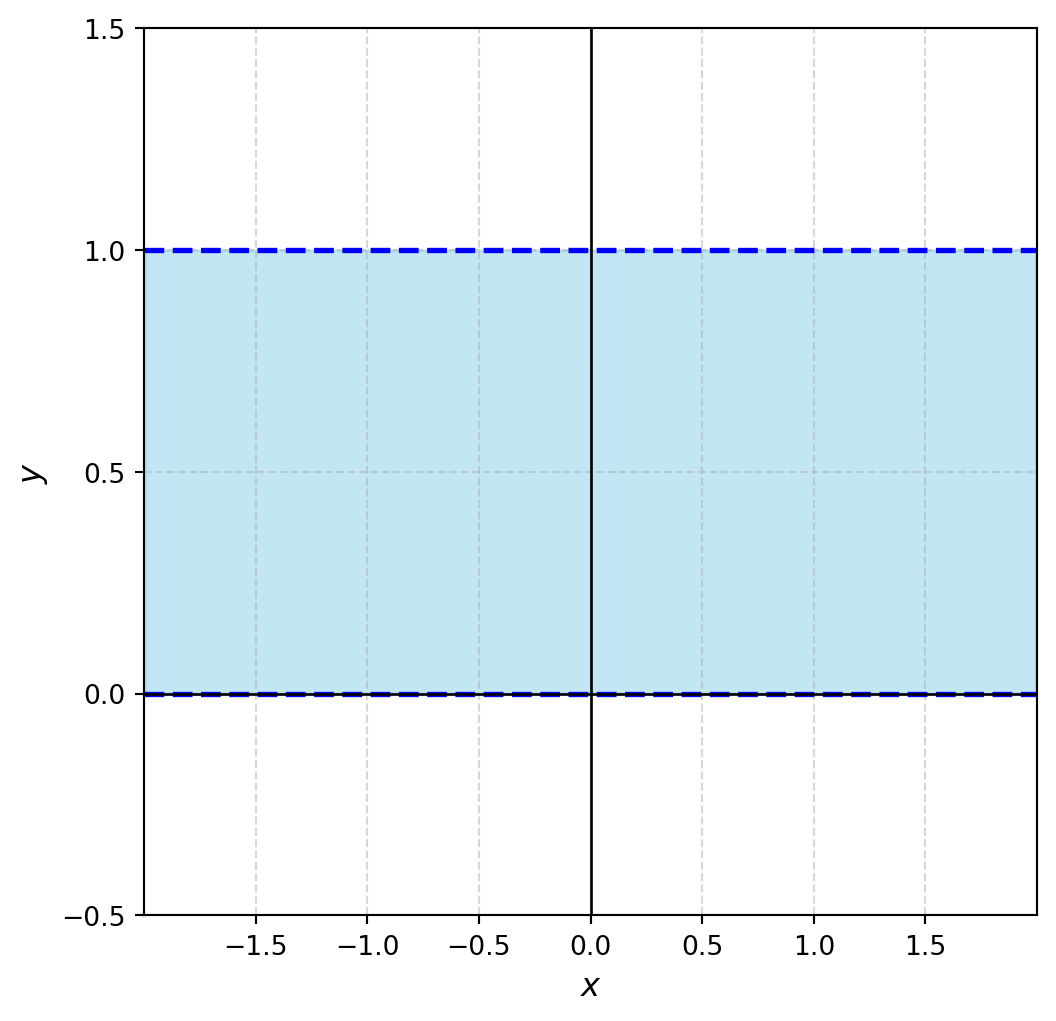
4. $\left\{(x,y)\in\mathbb{R}^2 : 0 < y < 1\right\}$
::: solution
Ouvert
```{python}
import matplotlib.pyplot as plt
import numpy as np
# Création de la figure et des axes
fig, ax = plt.subplots(figsize=(6, 6))
# Dessiner la région remplie entre x = -1 et x = 1, y entre 0 et 1
x_fill = np.linspace(-2, 2, 1000) # Points pour remplir le rectangle
y_bottom = np.zeros_like(x_fill) # Bas de la région y = 0
y_top = np.ones_like(x_fill) # Haut de la région y = 1
ax.fill_between(x_fill, y_bottom, y_top, where=(x_fill > -2) & (x_fill < 2),
color='skyblue', alpha=0.5, label='0 < y < 1')
# Tracer les segments horizontaux (inclus dans l'ensemble)
ax.hlines(y=0, xmin=-2, xmax=2, color='blue', linestyle='--', linewidth=2)
ax.hlines(y=1, xmin=-2, xmax=2, color='blue', linestyle='--', linewidth=2)
# Tracer les lignes verticales pointillées aux limites x = -1 et x = 1 dans y ∈ [0, 1]
# y_vertical = np.linspace(0, 1, 100) # y de 0 à 1
# ax.plot([-1] * len(y_vertical), y_vertical, 'b--', linewidth=2) # x = -1
# ax.plot([1] * len(y_vertical), y_vertical, 'b--', linewidth=2) # x = 1
# Ajouter les axes x et y qui s'intersectent en (0,0)
ax.axhline(0, color='black', linewidth=1) # Axe des x
ax.axvline(0, color='black', linewidth=1) # Axe des y
# Configuration des limites et des graduations
ax.set_xlim(-2, 2)
ax.set_ylim(-0.5, 1.5)
ax.set_xticks(np.arange(-1.5, 1.6, 0.5)) # Graduations sur x
ax.set_yticks(np.arange(-0.5, 1.6, 0.5)) # Graduations sur y
# Étiquettes des axes
ax.set_xlabel('$x$', fontsize=12)
ax.set_ylabel('$y$', fontsize=12)
# Affichage de la grille pour une meilleure lisibilité
ax.grid(True, linestyle='--', alpha=0.5)
# Affichage du graphique
plt.show()
```
:::
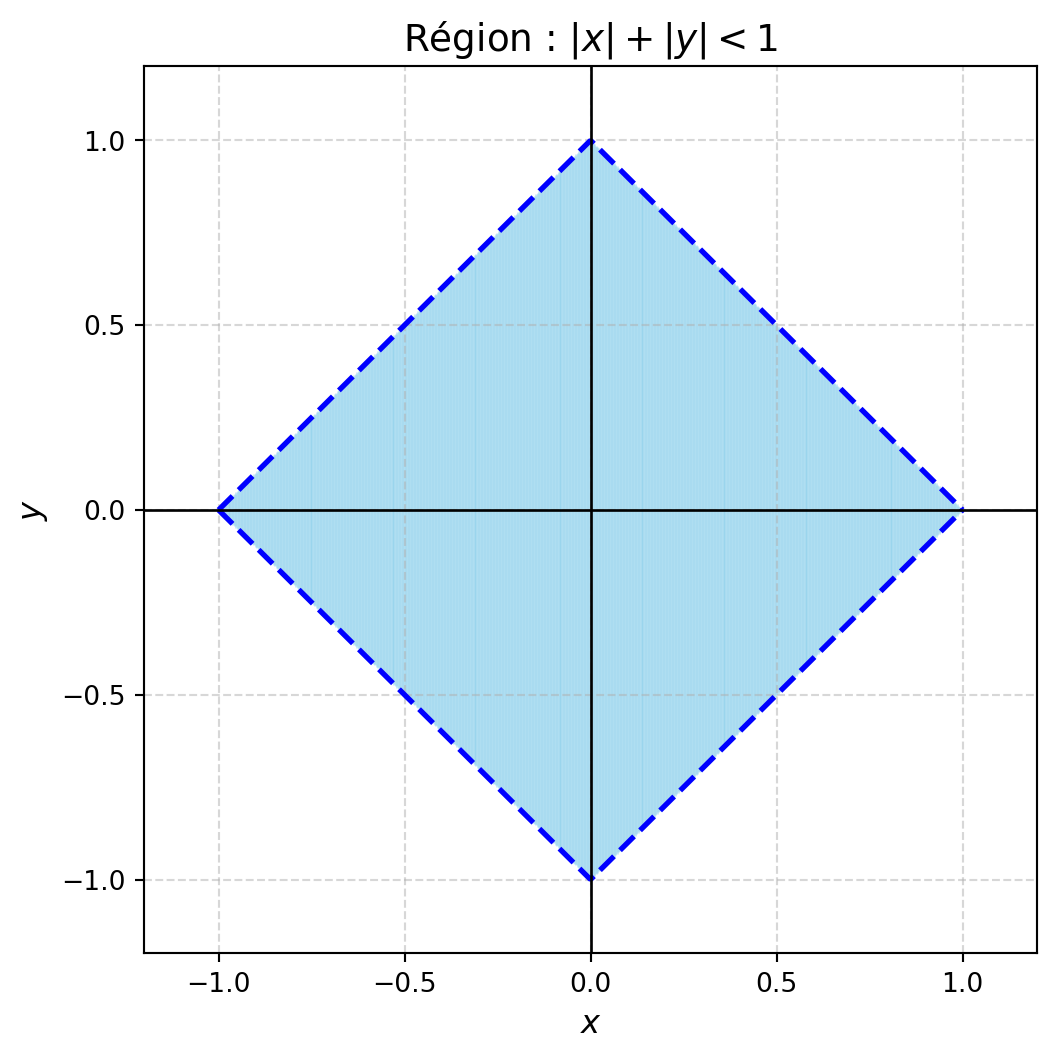
5. $\left\{(x,y)\in\mathbb{R}^2 : |x|+|y| < 1\right\}$
::: solution
Ouvert et borné
```{python}
import matplotlib.pyplot as plt
import numpy as np
# Création de la figure et des axes
fig, ax = plt.subplots(figsize=(6, 6))
# Générer les points pour tracer la frontière |x| + |y| = 1
x = np.linspace(-1, 1, 500) # Intervalle pour x
y1 = 1 - np.abs(x) # y positif pour la frontière
y2 = -(1 - np.abs(x)) # y négatif pour la frontière
# Tracer la région remplie à l'intérieur de la frontière
x_fill = np.linspace(-1, 1, 500)
for x_i in x_fill:
ax.fill_between([x_i], -(1 - abs(x_i)), 1 - abs(x_i), color='skyblue', alpha=0.5)
# Tracer la frontière en pointillés (|x| + |y| = 1)
ax.plot(x, y1, 'b--', linewidth=2) # Partie supérieure
ax.plot(x, y2, 'b--', linewidth=2) # Partie inférieure
# Ajouter les axes x et y qui s'intersectent en (0,0)
ax.axhline(0, color='black', linewidth=1) # Axe des x
ax.axvline(0, color='black', linewidth=1) # Axe des y
# Configuration des limites et des graduations
ax.set_xlim(-1.2, 1.2)
ax.set_ylim(-1.2, 1.2)
ax.set_xticks(np.arange(-1, 1.1, 0.5)) # Graduations sur x
ax.set_yticks(np.arange(-1, 1.1, 0.5)) # Graduations sur y
# Étiquettes des axes
ax.set_xlabel('$x$', fontsize=12)
ax.set_ylabel('$y$', fontsize=12)
ax.set_title(r"Région : $|x| + |y| < 1$", fontsize=14)
# Affichage de la grille pour une meilleure lisibilité
ax.grid(True, linestyle='--', alpha=0.5)
# Affichage du graphique
plt.show()
```
:::
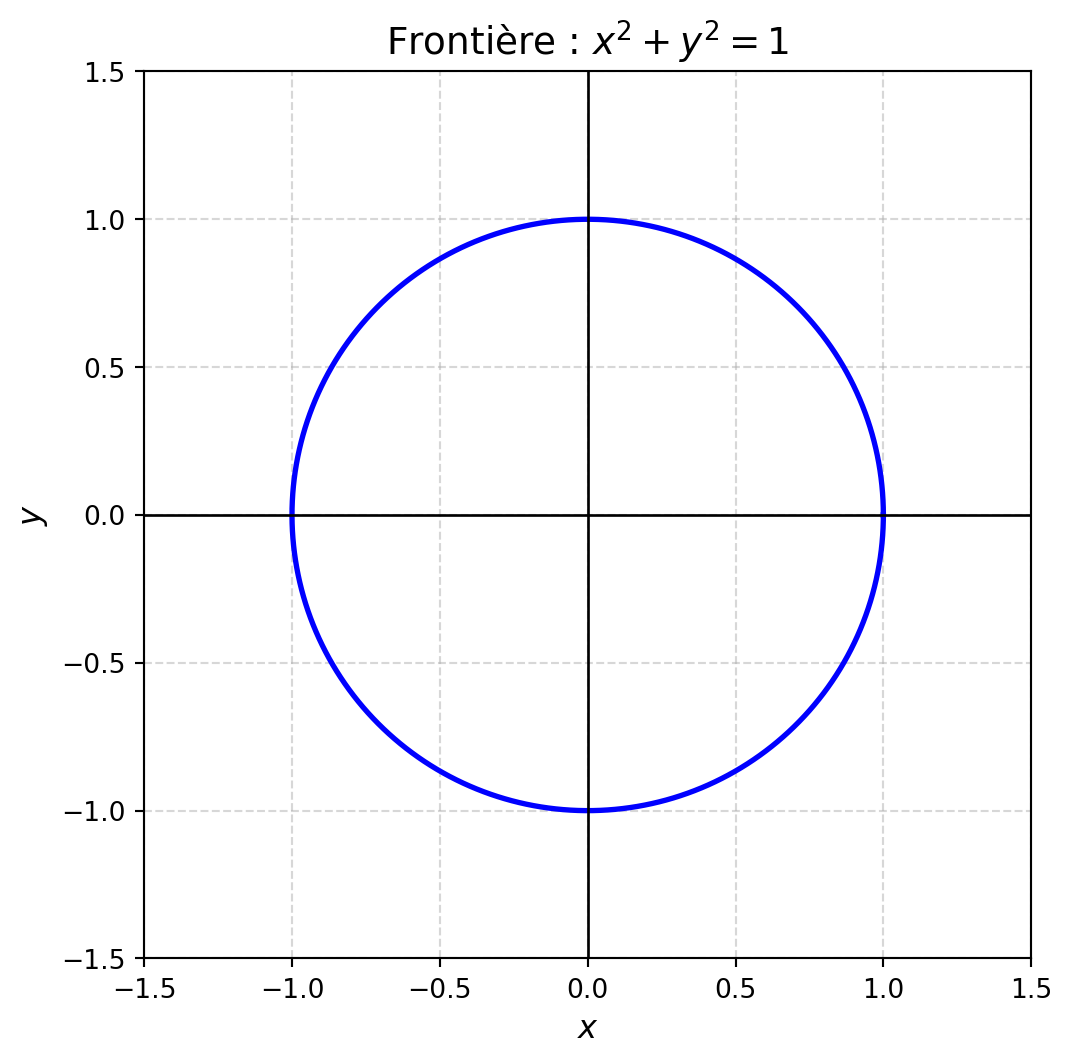
6. $\left\{(x,y)\in\mathbb{R}^2 : x^2 + y^2 = 1\right\}$
::: solution
Borné, fermé et compact
```{python}
import matplotlib.pyplot as plt
import numpy as np
# Création de la figure et des axes
fig, ax = plt.subplots(figsize=(6, 6))
# Paramètres pour tracer le cercle x^2 + y^2 = 1
theta = np.linspace(0, 2 * np.pi, 1000) # Paramètre pour la circonférence
x = np.cos(theta) # Coordonnées x sur le cercle
y = np.sin(theta) # Coordonnées y sur le cercle
# Tracer la frontière du cercle en pointillés
ax.plot(x, y, linestyle='-', color='blue', linewidth=2, label=r'$x^2 + y^2 = 1$')
# Ajouter les axes x et y qui s'intersectent en (0,0)
ax.axhline(0, color='black', linewidth=1) # Axe des x
ax.axvline(0, color='black', linewidth=1) # Axe des y
# Configuration des limites et des graduations
ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-1.5, 1.5)
ax.set_aspect('equal') # Assure un repère orthonormé
ax.set_xticks(np.arange(-1.5, 1.6, 0.5)) # Graduations sur x
ax.set_yticks(np.arange(-1.5, 1.6, 0.5)) # Graduations sur y
# Étiquettes des axes et titre
ax.set_xlabel('$x$', fontsize=12)
ax.set_ylabel('$y$', fontsize=12)
ax.set_title(r"Frontière : $x^2 + y^2 = 1$", fontsize=14)
# Affichage de la grille pour une meilleure lisibilité
ax.grid(True, linestyle='--', alpha=0.5)
# Affichage du graphique
plt.show()
```
:::
## Question 7
Soit $(E,d)$ un espace métrique et soit $f:E\rightarrow E$, une contration. Montrez que $f$ est continue. Rappelons qu'un fonction $f$ est continue en $x_0$ si pour tout $\varepsilon>0$, il existe $\delta>0$ tel que
$$x\in E~\text{et}~d(x_0,x)<\delta\Rightarrow d(f(x_0),f(x))<\varepsilon.$$
## Question 8
Assurez-vous de pouvoir définir sans aide chacun des objets mathématiques ci-dessous. Vérifiez vos réponses dans les notes de cours.
- Une contraction sur $\left(\mathbb{R}^2,d_E\right)$.
- Un sous-ensemble borné de $\left(\mathbb{R}^2,d_E\right)$.
- Un sous-ensemble fermé de $\left(\mathbb{R}^2,d_E\right)$.
- Un sous-ensemble compact de $\left(\mathbb{R}^2,d_E\right)$.
- Une métrique sur un ensemble $X$.
- Un espace métrique.
- Une suite de Cauchy dans un espace métrique $(X,d)$.
- Un espace métrique complet.